使用DAC对开关电源或线性电源的反馈网络注入微小电流,从而达到控制输出电压的技术,我想应该不是什么秘密了。但网络上的文章都是泛泛地谈一下原理,根据不同的电阻配置计算出电压调节范围,有种根据结果推导原因的感觉,而不是根据原理去设计出结果。而我很早就开始使用这个方法,当时为了迎合公司快速开发的需求,也没有对这个电路深入思考,只记得拉了一个excel表,随便选几个值看哪个最接近设计要求。所以我觉得有必要重新整理记录一下设计方法。
废话不多说,直接进入主题:
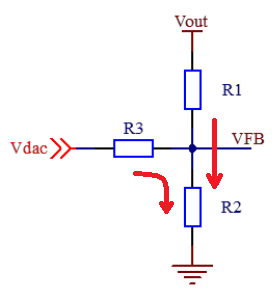
假设电源的反馈网络工作在平衡状态,即VFB电位为DC-DC(或LDO)芯片的内部参考电压。根据基尔霍夫电流定律
\[I_{R_2}=I_{R_1}+I_{R_3}\] \[\frac{V_{F B}}{R_2}=\frac{V_{\text {out }}-V_{F B}}{R_1}+\frac{V_{\mathrm{dac}}-V_{F B}}{R_3}\] \[V_{\text {out }}=V_{F B}\left(\frac{R_1+R_2}{R_2}+\frac{R_1}{R_3}\right)-V_{\mathrm{dac}} \frac{R_1}{R_3}\] 可得出 Vout 与 Vdac 是负线性关系,确定与坐标轴的两个截距就能确定输入输出关系。
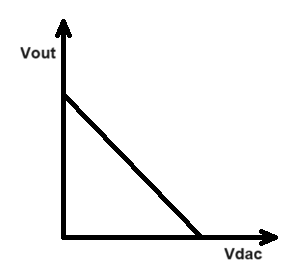
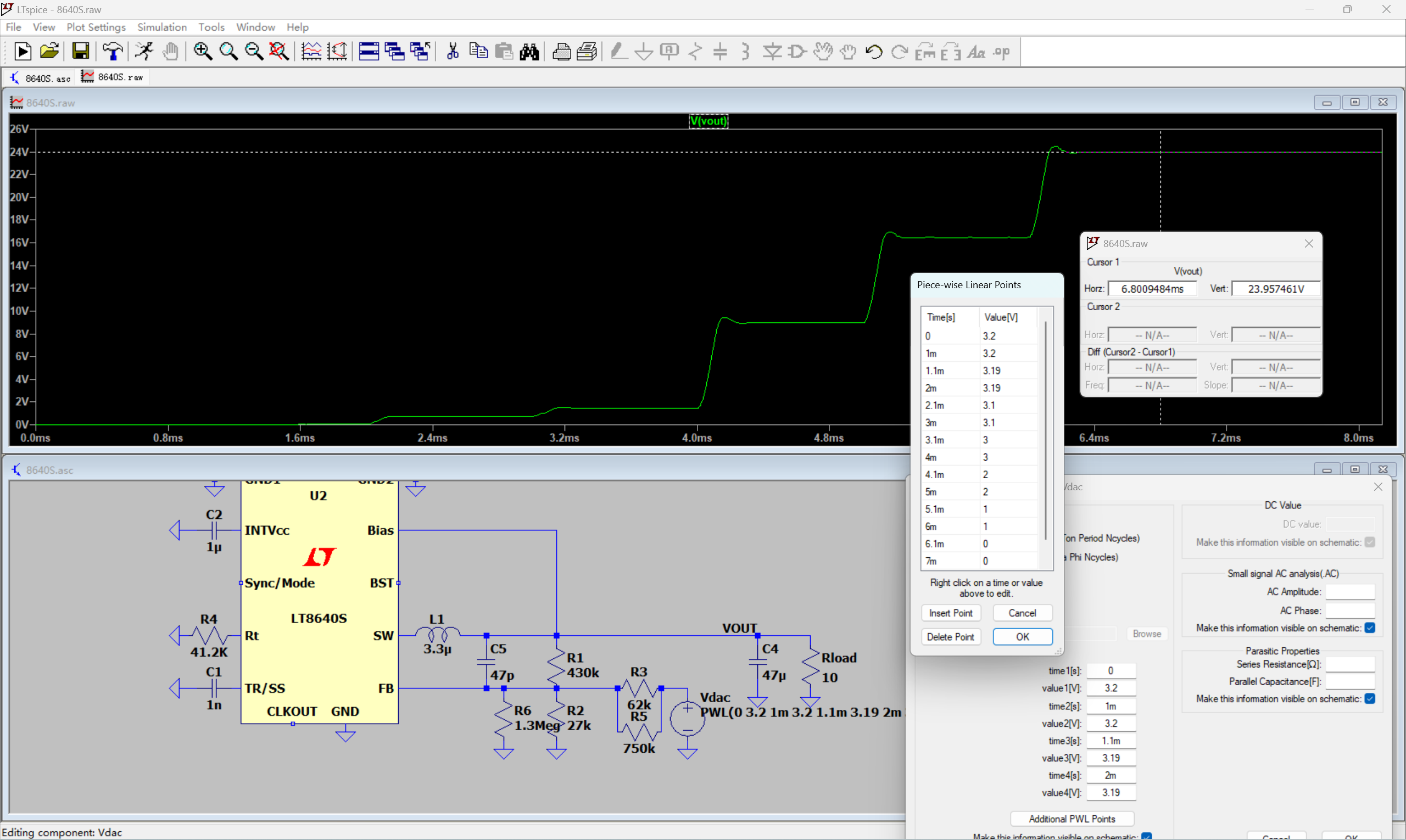
一般会将 Vout 输出最低值设计到0V,即使DC-DC在极低输出电压下(占空比非常小)会不稳定。最大值根据芯片和需求取,以LT8640S这颗芯片为例,设计输出电压范围0~24V,控制信号为0~3.2V的电压,可以得到:
边界条件1:Vdac = 3.2V时, Vout = 0,即
\[\begin{gathered} \left(\frac{R_1 R_3+R_2 R_3}{R_1 R_2}+1\right) V_{F B}=3.2 \mathrm{~V} \end{gathered}\] 边界条件2:Vdac = 0 时,有 R1 和 R2//R3 组成的分压网络,可以取 R1=430kΩ ,R2//R3=18.1kΩ,即
\[\frac{R_2 R_3}{R_2 + R_3} =18100 \mathrm{Ω}\] 根据上面两个等式用数学软件解出:
\[\begin{aligned} & R_1=430 \mathrm{k} \Omega \\ & R_2=26.4575 \mathrm{k} \Omega \\ & R_3=57.2994 \mathrm{k} \Omega \end{aligned}\] 使用E24系电阻并联,在LTspice中仿真得到,输出电压最高23.95V。
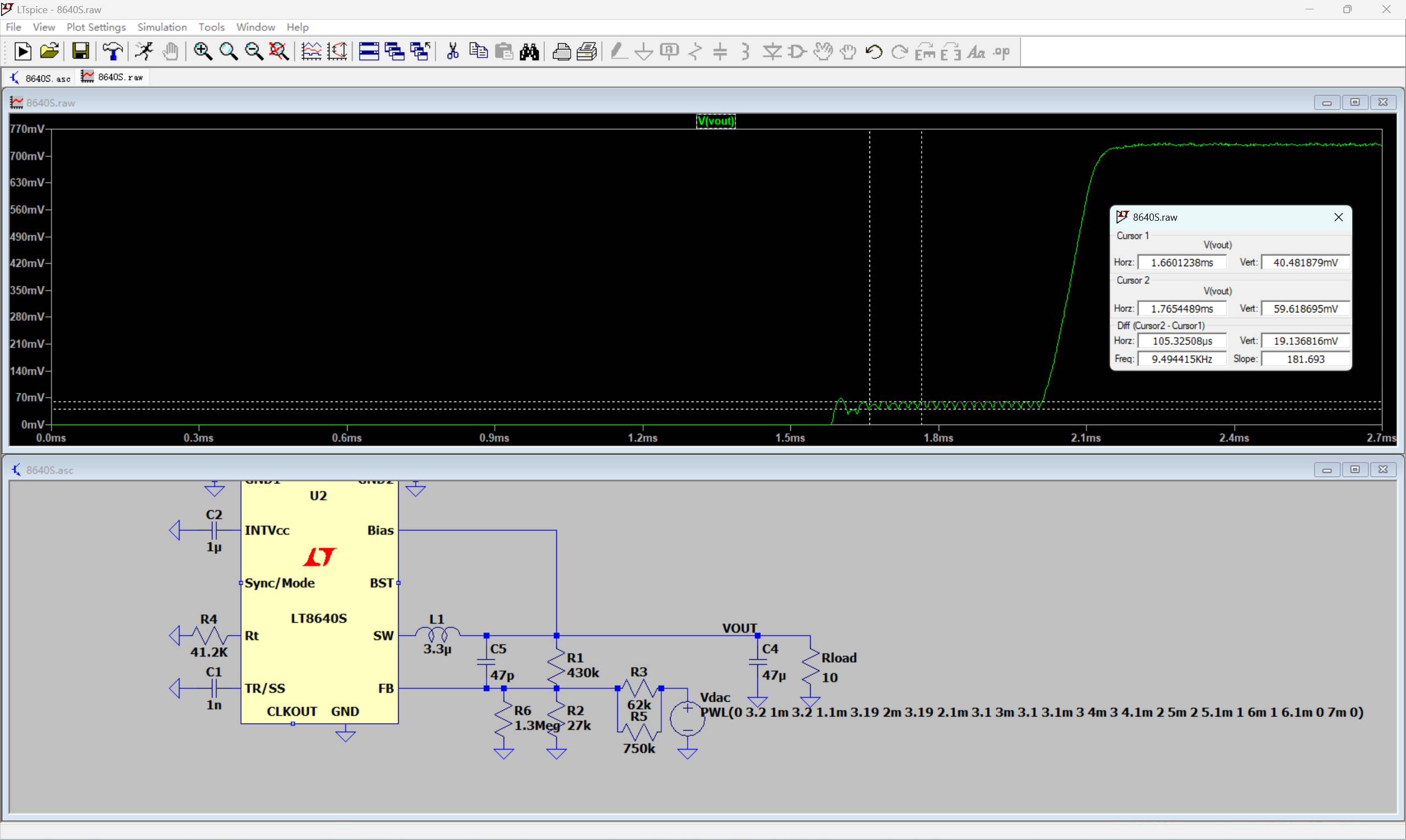
在输出电压低至50mV时,纹波约20mV,不要觉得20mV很小了,这是ADI的Silent Switcher 2架构!纹波几mV才是正常的!